The primary reason for investing is to make returns for wealth creation and accumulation. Which returns would you rather have, 10% or 15%?
The truth is the higher the returns, the better, all factors held constant. Different formulas are used to calculate returns. However, we will deal with the average annualized return formula, AAR, and its effect on investment decisions.
AAR formula calculation and working
AAR is a historical measure of the returns from an investment vehicle, net of the asset’s administrative and operational expenses. In addition, average annualized returns don’t consider any sales charges and/or commission fees. Therefore, it measures how much money an investment asset has lost or made over a specified period, usually more than a single year.
Whereas the average annualized return primarily measures an asset’s profitability in the long term, investors should always interrogate the numbers-crunching up the overall figure.
This analysis reveals any inconsistency in the short-term returns facilitating better decision-making. For example, the annualized 3-year returns of the SPY might be 15.75%. However, the yearly returns resulting in this 15.75% might be +30%, +25%, -7.75%.
What does this mean to the investor?
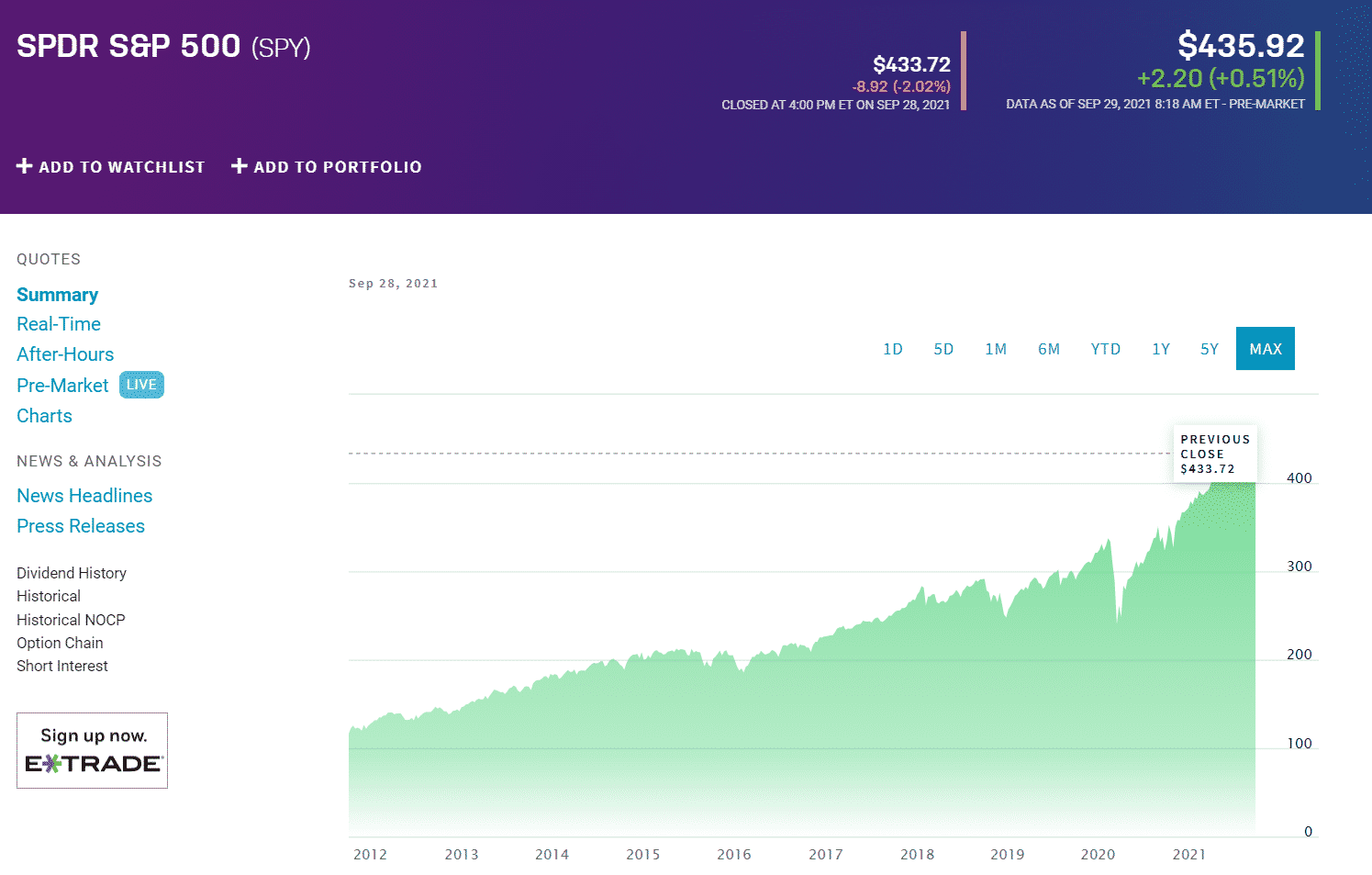
SPDR S&P 500 (SPY)
A look at the investment asset’s management and operations might reveal why short-term returns are so inconsistent, which ensures better anticipation in the future for hedge strategies in times of downturn.
In the example above, we have used a simple average to arrive at the 3-year returns. However, there are other factors to consider in the investment world, calling for a much more sophisticated algorithm for calculating annualized returns. Among these factors is the compounding effect of returns referred to as the compound annual growth rate, CAGR.
Considering CAGR, what is the annualized returns formula?
[(1+r1) x (1+r2) x (1+r3) x … x (1+ri)] (1/n) – 1
Where “r” is the annual rate of return, and “n” is the number of years in the period under review.
For example, an investment purchase of 200 MJ ETF shares at $50 each, held for three years, returns 30% in the current year, loses 7.75% next year, and then rises by 25% in the third year after the initial investment.
ETFMG Alternative Harvest ETF (MJ)
What is the AAR during the three years that an investor holds these ETF’s shares?
AAR= [(1+r1) x (1+r2) x (1+r3) x … x (1+ri)] (1/n) – 1
Here, r1=30%, r2=-7.75%, r3=25%, and n is 3.
[{(1+30%) x (1+-7.75%) x (1+25%)}1/3-1] x 100
[(1.3 x 0.9225 x 1.25) 1/3 -1 x 100
(3.4725) 1/3 -1 x 100 = 14.45%
Therefore, an investment in MJ ETF shares would yield a 14.45% return on investment for the three years.
Assuming that the rate of return is not available, but you have access to the dollar value of the returns generated, the average annualized return formula changes to:
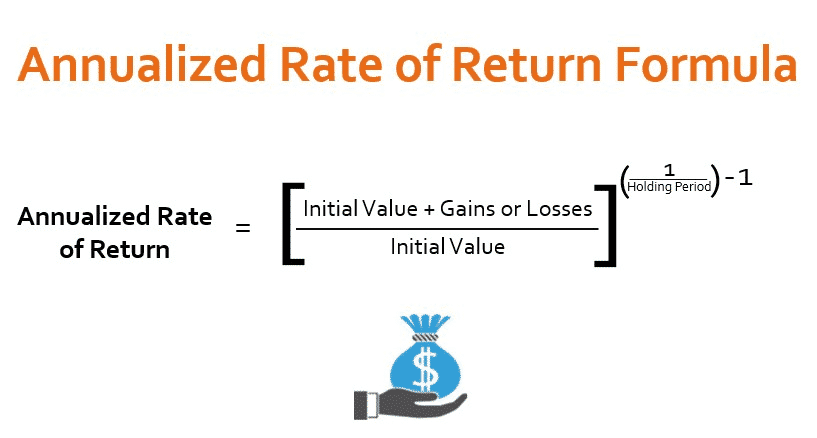
AAR = [(Final Value of Investment/Initial value of investment) (1/n) – 1] x 100
Where “n” is the number of years to be annualized.
Using the previous MJ example, a 20 shares investment at $50 per share results in a total investment value of $1000. Suppose holding the shares for three years coincides with market upturn resulting in quarterly dividends of $0.35 per share for the period and an increase in share price. If an investor sells the 20 shares at this point and MJ share price has appreciated to $53, what is the rate of return for these three years?
Initial value of investment = $50 x 20 = $1000
Final value of investment = dividends received + value of shares sold
Final investment value = ($0.35*12)20 + ($53*20) = 84 + 1060 = 1144
AAR = [(1144/1000) 1/3-1] x 100 = 4.59%
In the second scenario, the average annualized return for the three years is 4.59%.
The second formula takes into account all the indicators that affect the average annualized returns:
- Share price
- Dividends
- Capital gains distribution
AAR components
Share price
It is either appreciated or decline, affecting the overall value of the held investment asset. As share prices fluctuate, they influence the overall average annualized return, either as individual assets or as part of a pooled investment vehicle. Fluctuating share prices are the reason for ETF and mutual fund rebalancing to ensure the cumulative AAR objective is always within sight.
Dividends
Dividends distributed to shareholders of an asset influence the AAR value while also impacting its net asset value. Dividends can either be reinvested or taken as income to fund other projects. Depending on the management of an investment asset, they are either distributed quarterly, semiannually, or annually. The distributions form the dividend yield component of the AAR formula.
Capital gains distribution
Capital gains are the realized profits or losses in the AAR formula from selling the shares held. These capital distributions, similar to dividends, can either be received in cash or as additional shares for reinvestment. Capital gains are a taxable income stream for investors.
Final thoughts
This formula helps compare different investment options of the same category. This comparison ensures investment in assets that align with individual investment objectives and risk tolerance levels. With compounding, the AAR formula helps investors analyze returns from a holistic viewpoint facilitating better decision making.











Comments